计算机系统中信息数据的处理

前言

本文同样地是整理和归纳《深入理解计算机系统》这本书的内容，但本文不会继续长篇大论地去将所有内容都总结，而是总结笔者认为容易遗忘或混淆或表述不清的内容。

字

首先字这个概念对于学习过《计算机体系结构》或《操作系统》的同学都不陌生，但是笔者对于这个概念很容易遗忘，所以笔者还是记录下来。

总的来说：字长决定了虚拟地址空间的最大大小。也就是说，对于一个字长为 w 位的机器而言，虚拟地址的范围为 0 ～ $2^w-1 $，程序最多访问 $2^w$ 个字节。

如果一台计算机的字长为32位，这就限定了虚拟地址空间为4GB。也就是说，即使你的主存容量再大，处理器也只能寻址4G的范围，同样的道理，在嵌入式中，8位机的概念就是字长为8位的微型处理器。

现在市面上有许多32位，64位机器，在不同机器之间程序会遇到数据长度，寻址能力等方面的挑战，一个强大的程序，应该兼容不同的机器。

数据大小

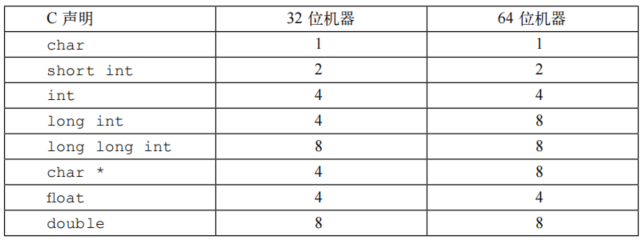
size of data

可以看到，在C语言中，数据类型在不同的字长的机器上占有不同的字节数，程序员应该力图使它们的程序在不同的机器和编译器上是可移植的，可移植性的一个方面就是程序堆不同数据类型的确切大小不敏感。

布尔代数

布尔代数实际上就是围绕数字0与1建立起来的一种代数体系，以研究逻辑推理和基本原则。

布尔代数只有0和1两个数，拥有与（&）、或（|）、非（~）、异或（^） 等运算，且运算间也遵循某种分配律和交换律

位级运算

在这里我们值得一提的是：在异或（^）运算中，我们需要注意到：a^a=0以及a^b^a=b

正是由于异或拥有这种神奇的性质，我们可以完成以下脑经急转弯。

请设计一个程序，在不适用第三个变量的情况下，交换x与y的值

1
2
3
4
5
6


void inplace_swap(int *x, int *y)
{
    *y = *x ^ *y; // step1
    *x = *x ^ *y; // step2
    *y = *x ^ *y; // step3
}

从上面这个函数可以看出，在step1时，y现在存储的值时 x ^ y ，在step2时，x 的值变为 x^ x ^ y = y这是根据a^b^a=b的运算规则，step3同学们可以自己算一下。

a^b^a=b这是一个运算规则而非定理，即，这并非人为规定，而是客观规律。我们尝试以下运算

a = 0110 0101

b = 1100 1011

根据异或的运算规则，相同则为0，不同则为1

我们设c = a ^ b = 1010 1110

此时再用c ^ a 得到

d = c ^ a = 1100 1011

你会发现，d = b ，即 a ^ b ^ a = b

除此之外，还有一个例题非常有意思

bis(位设置)：输入一个数据字x和一个掩码字m，生成一个结果z，z是由掩码m的位来修改x得到的，这种修改是在m为1的每个位置上，将z对应的位置设为1

bic(位清除)：输入一个数据字x和一个掩码字m，生成一个结果z，z是由掩码m的位来修改x得到的，这种修改是在m为1的每个位置上，将z对应的位置设为0

为了清楚因为这些运算与 C 语言位级运算的关系，假设我们有两个函数 bis 和 bic 来实现位设置和位清除操作。只想用这两个函数，而不使用任何其他 C 语言运算，来实现按位 | 和 ^ 运算。填写下列代码中缺失的代码。提示：写出 bis 和 bic 运算的 C 语言表达式。
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
// 你可以使用的函数
int bis(int x, int m);
int bic(int x. int m);
// 完善下列函数
int bool_or(int x,int y){
    int result = _______;
    return result;
}
int bool_xor(int x, int y){
    int result = _______;
    return result;
}

我们可以根据说明，模拟一下bis函数的运行输入输出：

当x = 0110 0101 m = 1100 1011时，

根据bis的说明，m的某一位为1时，则x对应的位被修改为1，其它不变

那么，res = bis(x,y) 则 res = 1110 1111

根据bic的说明，m的某一位为1时，则x对应的位被修改为0，其它不变

那么， res = bic(x,y) 则 res = 0010 0100

那么， res = bic(y,x) 则 res = 1000 1010

根据上面的演算，我们可以发现，当你使用bis时，则x与m两者都是0的位才为0，否则即为1。当你使用bic时，则仅有m为0时且x为1时，才为1。

那么或运算就好办了，因为或运算的规则就是只要有1则为1，逆命题就是两者为0才为0，即bis运算

则第一个函数为：

1
2
3
4


int bool_or(int x,int y){
    int result = bis(x,y);
    return result;
}

异或运算的规则为，只要不同则为1，否则为0。根据bic运算，当你使用bic时，则仅有m为0时且x为1时，才为1，可以得到不同的其中一种情况，即m为0且x为1，还要第二种情况，m为1且x为0，那么只需要将m与x的位置调换，在运算以此即可获得，然后将两者进行或预算，也就是bis运算即可。

1
2
3
4


int bool_xor(int x, int y){
    int result = bis(bic(x,y),bic(y,x));
    return result;
}

掩码

在数据处理中的掩码与计算机网络中的掩码概念有所不同，在这里的掩码你可以理解为是一种滤波器，它可以将特定位的数据通过而屏蔽掉其它位的数据，如

掩码：0x0000FF 与 a : 0x123456 进行运算，则会得到

res = 0x000056

补码编码

跳过了无符号数的编码

在计算机中，有符号数的表示方式就是补码，将字中最高有效位定义为负权（negative weight），如

1011 = -1*$2^3$+0*$2^2$+1*$2^1$+1*$2^0$ = -8 + 0 + 2 + 1 = -5

在这种编码下，最高位变成了乘了一个-1，因此，在这种情况下，我们要考虑在有有符号数补码编码的情况下的几种特殊情况：

0000 = 0

1111 = -1

0001 = 1

1000 = -8

0111 = 7

在字长未4的情况下，有符号数的补码编码中，取值范围为[-8:7]，1111并非最小值，而是-1，1000才是最小值为-8，0111是最大值7

在0000，0001，0010，…，0111，1000，…，1111以此类推中，实际上的数值变化是，0，1，2，…，7，-8，-7，…，-1

由此我们可以看到，补码的范围是不对成的，即最小值没有与之对应的正数。这导致补码运算的某些特殊的属性，并且容易造成程序中细微的错误。

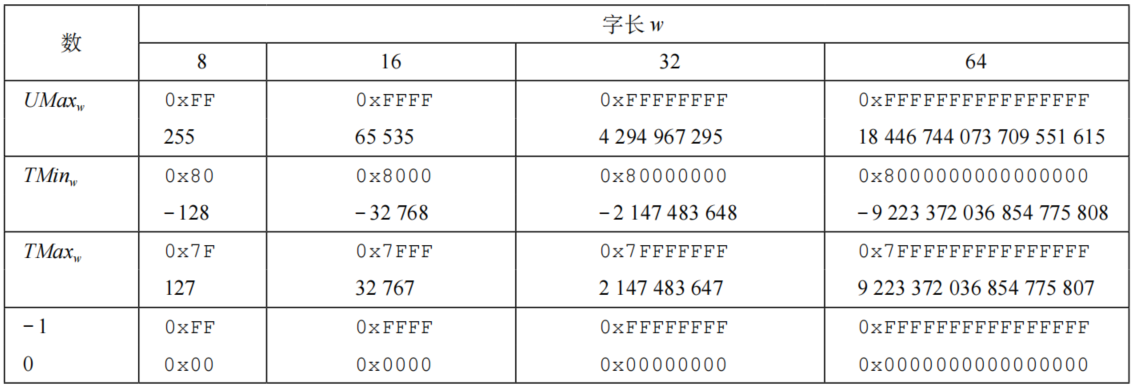
以下表格中，*$UMax_w$表示无符号数的最大值，$TMin_w$表示有符号数的最小值，$TMax_w$*表示有符号数的最大值

number

数据比较

由于 C 语言对同时包含有符号和无符号数表达式的这种处理方式，出现了一些奇特的行为。当执行一个运算时，如果它的一个运算数是有符号的而另一个是无符号的，那么 C 语言会隐式地将有符号参数强制类型转换为无符号数，并假设这两个数都是非负的，来执行这个运算。就像我们将要看到的，这种方法对于标准的算术运算来说并无多大差异，但是对于像 < 和 > 这样的关系运算符来说，它会导致非直观的结果。考虑比较式 -1<0U。因为第二个运算数是无符号的，第一个运算数就会被隐式地转换为无符号数，因此表达式就等价于4294967295U<0U，这个答案显然是错的。